Collectible card games including Hearthstone and Magic the Gathering regularly have overpowered cards printed due to the large number of cards created each year. Given that using overpowered cards can help in achieving a higher win rate, it is not surprising that players are constantly on the lookout for these cards. As a result, overpowered cards end up destroying the game diversity by being overplayed.
This blog post demonstrates how to find such overpowered Hearthstone cards automatically using statistical learning. This method can be used by a player to get an edge or by a game designer to check for a card design error.
The technique discussed in this post was originally used to analyze automatically 134 cards from the original release of Hearthstone in June 2014. Doing so revealed that Soulfire was the most overpowered card at that time.

Shortly after the release of this post, in September 2014, Blizzard nerfed Soulfire by increasing its cost as predicted by our algorithm. Thus, this validated the accuracy of our approach.
While the game card pool has evolved since this analysis was published, the underlying principles remain the same and our technique can easily be applied to Hearthstone’s current card pool and any other card game.
Last edit This post was last edited in October 2016. The introduction was fully rewritten to reflect the current state of the research.
This post is part of a series of posts about applying machine learning to Hearthstone. This series so far has the following posts:
- How to price Hearthstone cards: Presents the card pricing model used in the follow-up posts to find undervalued cards.
- How to find undervalued cards automatically: Builds on the pricing model to find undervalued cards automatically (this post).
- Pricing special cards: Showcases how to appraise the cost of cards that have complex effects, like VanCleef.
- Predicting your Hearthstone’s opponent deck: Demonstrates how to use machine learning to predict what the opponent will play.
- Predicting Hearthstone game outcomes with machine learning: Discusses how to apply machine learning to predict game outcomes.
The research discussed in this post was also presented at Defcon22 (slides and video).
Why overpowered cards exist and their effect on the game
Collectible card games require game designers to constantly create a large volume of new cards to sustain interest and keep the game profitable. For example, Hearthstone is updated with tens of new cards every three months. Given that all these new cards are manually designed on a very tight schedule, it is not surprising that often developers underestimate the power of their effect and release overpowered cards.

For Magic, the most famous example of such an overpowered card is Black Lotus released in 1993. More recently, the infamous Skullclamp card completely broke Magic’s meta-game in 2004 and triggered an emergency ban, as most decks at that time either played it or were designed to counter it.

While Hearthstone never “enjoyed” such overly broken cards, a few came close, including Warsong Commander and the patron deck that broke the meta in 2015. Amazingly, Warsong Commander was not nerfed just once, but twice before they got it under control as illustrated above.
##Approach overview
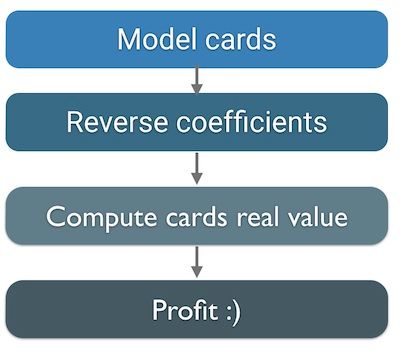
As illustrated above, finding undervalued cards is done in four steps:
Each card is converted to a linear equation that expresses its mana cost as a function of its attributes, as we did in the previous post.
The resulting set of card equations is treated as an over-determined system and the ordinary least-squares method is used to compute the attribute coefficients.
The attribute coefficients are used to compute the true value of the cards.
Finally, we compare the computed true value with the cost assigned by Blizzard. The cards that have the largest difference between their true value and their face value are the most under- or overvalued.
While this process might seem complicated, in practice it requires less than 100 lines of code when the cards have been converted into the linear equation format. The example below should clarify how the overall approach works.
Before delving into the example, it is worth mentioning that I spent most of my time writing the parser that analyzes the text of each card to extract its attributes properly. To give you an idea of how tedious this part of the process is, just know that it took me a week of work to model the 134 cards used in this analysis. If you know how to code in Python and are interested in expanding the analysis, let me know :)
##A simple example
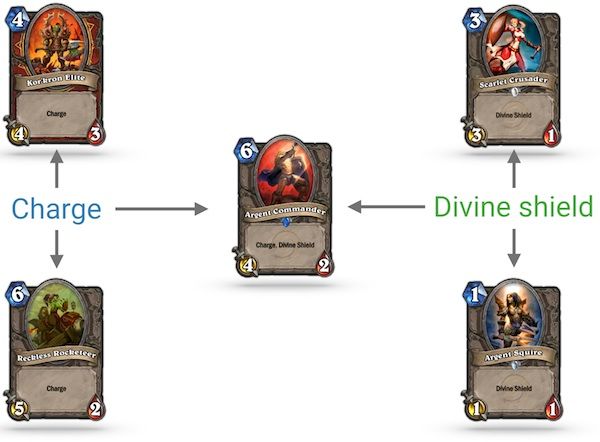
To explain how our approach works, let’s apply it to only five cards, so that it’s easier to follow. These cards were chosen to illustrate three key concepts that the method builds on:
- Cards that are undervalued compared to others: The algorithm works by comparing the sum of the cost of card attributes. A card imbalance happens when one attribute costs less in one card than another.
- The attributes must be on other cards too: If an attribute is used by only one card, then the algorithm can find how much mana it cost to get this attribute on the card. However, this attribute can’t be used to find undervalued cards as it is not used by any other cards. While this might seem like a huge restriction, it is not as bad as it seems as attributes can be combined as explained below. How to price cards with complex abilities, like VanCleef, is the subject of the next post. In our example, we have three cards with Charge and three with Divine Shield, so we are good to go.
- Attributes and abilities can be combined: The mana cost of a given attribute or ability is the same regardless of how many attributes the card has or their total cost. This allows us to price cards that have a unique combination of attributes as long as those attributes are used by other cards. In our example, Argent Commander has a combination of Charge and Divine Shield that makes it unique. However, we can still evaluate it as we have two other cards with Charge (Kor’Kron and Rocketeer) and two other cards with Divine Shield (Argent Squire and Scarlet Crusader).
###Step 1: Modeling cards
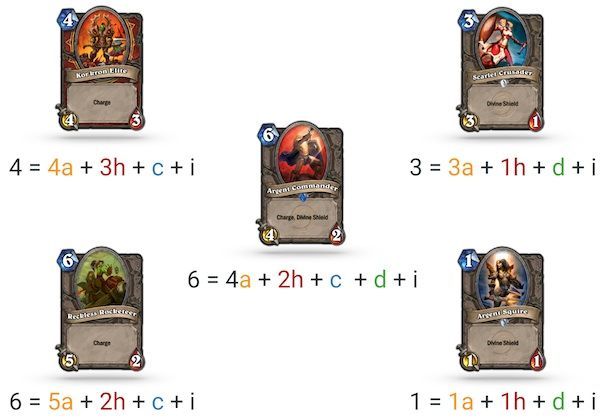
During the first step, as illustrated above, we first convert each card into a linear equation as explained in the previous post. Then, we combine those equations into a matrix, as visible on the right side of the figure below.
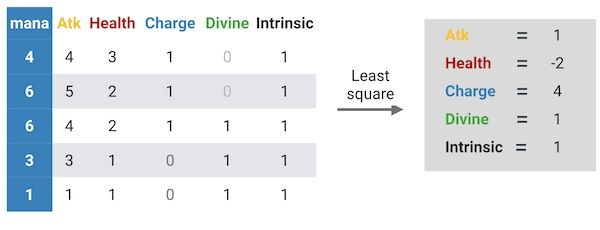
Each row in the matrix is a card, where the first column in blue denotes its mana cost and each subsequent column the value of a given attribute.
For example, the first row is the Kor’Kron card. Accordingly, we put the value 4 in the mana column as the card costs 4. We put the value 4 in the atk column as the card has 4 attack points and 3 in health as the card has 3 health points. The charge column gets a 1 as Divine Shield is present and the divine column gets 0 as Kor’Kron doesn’t have the Divine Shield attribute. The intrinsic value is always set to 1, as it is used to model the cost of owning the card.
Note that in the example, for simplicity, we model only if an ability (Charge or Divine Shield) is present or not: we use 1 for its presence and 0 for its absence. However, in reality things are not that simple.
As pointed out first by Niels, some abilities clearly depend on other characteristics and should be modeled taking those dependencies into account (almost like a kernel trick).
After going back and forth with Niels, we ended up modifying the current model to make Charge a factor of the attack value of the card (e.g., 4c for Argent Commander) as the charge value clearly depends on the attack power. For the other abilities, it is less clear how they should be modeled, so if you have any opinions or ideas, let me know Twitter.
###Step 2: Reversing the coefficients
Using the ordinary least-squares method, we can use our matrix to figure out the coefficient cost for our five attributes as illustrated on the right side of the figure above. This allows us to know how much it cost to have a single point of a given attribute on the card.
In our example, 1 point of attack costs 1 mana, a health point costs -2 mana, Charge costs 4 mana and Divine Shield costs 1 mana. These example coefficients are a little weird because we didn’t evaluate enough cards to get meaningful values. In reality, a health point costs 0.4 mana, as we will see below.
###Step 3: Compute real card values
Now that we know the cost of an attribute point, we can compute the true cost of a card by replacing the coefficients by their values and then multiplying them by the number of points before summing them.
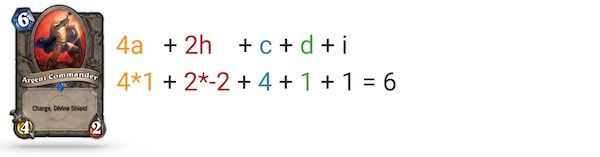
Doing so for Argent Commander, as illustrated above, gives us a true value that is the same as its face value: 6. Therefore, we conclude that Argent Commander has a fair price.
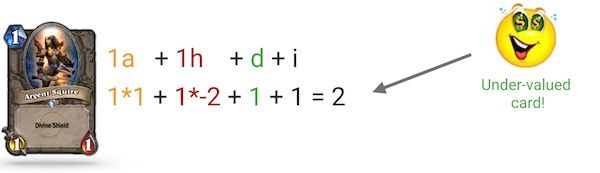
Doing the same analysis for Argent Squire shows us that it is an undervalued card. As visible above, while the face value of Argent Squire is 1 mana, its computed true value is 2. The difference between the two prices (1 mana) clearly indicates that the card is currently undervalued by 50%, at least in our example.
In reality, as we will see below, when our method is applied on a larger pool of cards, Argent Squire is not that much undervalued. That being said, it is still one of the most undervalued cards according to our algorithm.
##Computing attribute coefficients
Applying the approach described above to the 134 Hearthstone cards that I modeled, gave us the following mana cost for the various game abilities:
Positive attributes
| Effect | Cost per point |
|---|---|
| Destroy Minion | 5.33 |
| Draw Card | 1.84 |
| Board Damage | 1.84 |
| Divine Shield | 1.40 |
| WindFury | 1.19 |
| Freeze | 1.02 |
| Silence | 0.83 |
| Damage | 0.82 |
| Stealth | 0.61 |
| Durability | 0.60 |
| Attack | 0.57 |
| Taunt | 0.51 |
| SpellPower | 0.46 |
| Health | 0.40 |
| Heal | 0.34 |
| Self Hero-Heal | 0.34 |
| Charge | 0.33 |
Looking at the attribute costs yields a few insights about their value. The best example is the costliest ability, Destroy Minion, which is used, for example, in the Naturalize card. Its cost of 5.33 means that you start to get value out of it when you nuke a card that costs 6 mana or more.
Comparing coefficients also gives interesting insights: The one that struck me the most is that a health point is 30% cheaper than an attack point.
Negative attributes
We also have coefficients that reduce the cost of a card as they are a disadvantage. That our algorithm infers a negative value for a drawback ability is another sign that our approach is sound.
| Effect | Cost per point |
|---|---|
| Opponent Draw Card | -1.98 |
| Discard Cards | -1.25 |
| Overload | -0.83 |
| Self Hero Damage | -0.27 |
As reported in the table above, having the opponent draw a card gives by far the biggest reduction, which I find fair. What I find a little imbalanced is that discarding a card reduces the cost of the card by 1.25 mana, whereas the mana cost for drawing a card is 1.84.
##Finding undervalued cards
We’re almost done! All we need to do now is to use our computed coefficients to re-compute the true value of the cards, and then order them by the difference between their face value and true value.
This method allows us to find the most underpriced cards (overpowered cards) and the most overpriced cards. The cards with a true value higher than their face value are undervalued, and those with a true value lower than their face value are overpriced. The graph below shows how the true value vs. face value compares for all our cards.
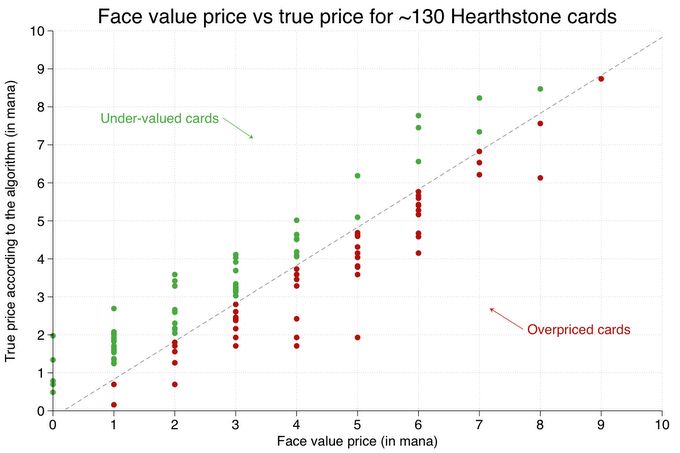
As expected, most of the cards are very close to the neutral line (represented in dots), where the true price roughly matches the face value. Because we force a card to be either undervalued (above the line) or overpriced (below the line), every card appears in one or other category. What is really important are the outliers, which are clearly far away from the line and represent the obvious under- and overvalued cards. As visible in the graph, there are quite a few!
###Which are the overpowered cards?
To get a list of the most undervalued cards, I normalized the difference between their face value and their true value (represented in the green gem) by dividing the difference by their face value. The most undervalued cards are reported below.
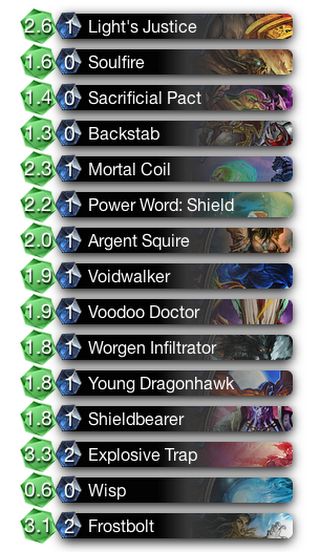
From this list, I feel that Soulfire (nerfed in 2014), Argent Squire, Power Shield and Mortal Coils are clearly undervalued cards. Making Frostbolt cost an extra mana is also something that I can see as possible.
Overall, looking at this list makes clear why zoo decks are so powerful, as they use a lot of undervalued cards. Finding this correlation is a good hint that, while imperfect, our model is going in the right direction and it will provide a strong foundation for rigorously analyzing the value of Hearthstone cards.
By way of disclaimer, I’ll be the first to say that the code I wrote isn’t perfect and the analysis has some weird results. If you feel like improving it, let me know.
Overall, representing cards as an over-determined system of equations lets us find the best “deal” for cards by revealing which are the most undervalued. It’s not perfect, but it does give us a systematic way to analyze the game rather than relying on intuition. In the next post, we’ll look at how to analyze cards that have unique effects or depend on the board state.
Thanks for reading this post to the end! If you enjoyed it, don’t forget to share it on your favorite social network so your friends and colleagues can enjoy it too.
To get notified when the next post is online, follow me on Twitter, Facebook, Google+. You can also get the full posts directly in your inbox by subscribing to the mailing list or the RSS feed.




